Some players treat the computer as gospel. After all, the computer has infinite computing power, perfect word knowledge, and can compute endgames and simulations with ease. It can play at lightning speed with consistency, and does not suffer from the same psychological or mental lapses as humans. It rarely makes a play that is obviously wrong, does a great job at leave evaluation, and can evaluate board openings better than any human. Some players believe that our goal as players should be to emulate top computer programs as blindly as possible.
Others are complete skeptics. Computers cannot possibly understand the intricacies of the game, accounting for opponent tendencies, board dynamics, or other complex concepts, they argue. They are slaves to their algorithm, biased far too much by points and leave without understanding the intricate nature of Scrabble to its fullest. They argue that computers are only capable of playing for valuation.
Both perspectives have a certain amount of validity to them if applied correctly. Simulations are dangerous and misleading when accepted blindly, but still provide useful information and is a useful tool that should not be ignored completely. So you might be thinking: “When are simulations useful?” To answer this question, it is important to understand the strengths and weaknesses of simulation.
Strengths of Simulation
Simulation is a great tool in positions where your opponent will frequently maximize equity. This occurs most often on open boards: in game situations with normal tile pools where board control, setups, etc. are not major factors. In these situations, simulation is almost always extremely accurate.
Many people find simulation to be a very useful instrument to help players improve and analyze play. Some of simulation’s strong points include:
• Simulations are good at maximizing valuation.
• Simulations are good at predicting an opponent’s bingo percentage. This can help you figure out which play will prevent the most bingos. This feature is enhanced by the implication engine, which allows you to input a range of strong racks to plot your opponent’s bingo percentage, and is displayed prominently in the details box.
• Simulations rarely recommend terrible plays. While simulations will not always find the best play, nearly any poor play will perform poorly after a simulation, since the computer will be able to look ahead and see the pitfalls of poor plays.
• Simulations are reliable during the (pre)endgame. They are extremely strong at permutation.
• Simulations can assess how often fishing plays and setups will succeed. This will help analyze the best play and develop heuristics to make this calculation over the board.
• Simulations can help you assess whether unusual plays with low equity have merit. If the play becomes much stronger after simulation, that play may be worth considering.
• Simulation can help you figure out which plays are more entropic than others. By observing each play’s standard deviations (in the details box) and employing proper entropy fundamentals, you can strike a good balance between valuation and entropy.
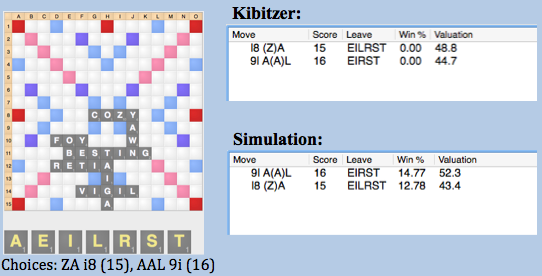As shown above, the kibitzer prefers ZA i8 over AAL. This is clearly incorrect, as most bingos that you draw next turn will not fit on the board after ZA unless your opponent opens the board on the next turn. Meanwhile, the bingos we draw after AAL are MUCH more likely to fit on the board, since they will often play hooking AALS. In the simulation, AAL clearly beats ZA.
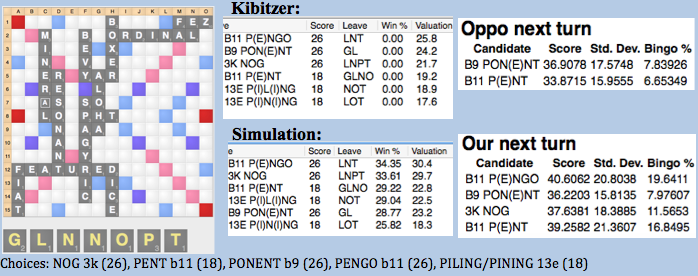
Here we can see that despite seeming like a strong play, PONENT does not perform so well in the simulation and is a weaker play than it might initially seem. This is because the GL leave is very weak on this board (as illustrated by the Our Next turn in the details box, it scores poorly even compared to leaves such as LNPT and GLNO) and the PO at b9 gives up over 3 points of expected value in overlaps (as seen in Oppo next turn of the Details box). The detail box thus elucidates some of the components of the position that make PONENT weaker than simple valuation would initially dictate.
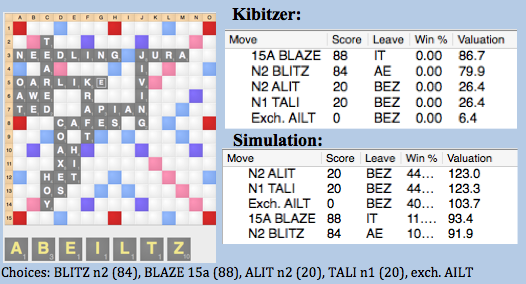
In this position, the J is stronger than normal due to the opening Y at 14h, G at j6, column o openings, and generally closed board, but simulation shows us that these openings are not enough to keep the J on the opening play. Here, simulation can be used to quantify the value of specific openings on the board. It is worth noting that if you are ahead, then keeping the J would be worth while as keeping the J leads to a significant drop in standard deviation.
Weaknesses of Simulation
With all these great tools and uses of simulation, what could possibly go wrong? Unfortunately, there are several types of positions where simulation can go awry. After all, simulations are not AI: they cannot think. They are merely calculators: they take in data and spit it back out, and sometimes those calculations are incorrect.
To look at why, we need to think about what exactly simulation does: it looks ahead at future plays and evaluates them using its kibitzer. For most positions, this is a valid approach, as the kibitzer is usually a pretty good estimator of future plays. But sometimes it’s not, and that can cause simulation to deliver some pretty wonky results. The kibitzer is not a good estimator (and can thus throw off the simulation engine) in the following situations:
- Positions that involve recursion. With certain fishing and setup plays, the benefit is not only in the possible plays next turn, but what is also possible on future turns. The kibitzer cannot take that into account since it is unable to use complex reasoning on future turns: it will burn case-S hooks immediately, play the J or Q that has a much higher-than-average tile equity too easily, and give up on fishing plays when they fail far too quickly. The simulation will never make the fishing or setup play next turn.
- Simulations do not use leave inference to make their decisions. As a result, they will often underestimate (or overestimate) their opponent’s ability to use the openings available on a given board.
- Likewise, simulations do not assume that your opponent will use leave inference. Simulations underestimate the general strength of your opponent’s rack. Unless they just played a bingo, your opponent usually has a better than average leave even without implication, since opponents also understand the value of keeping a good leave.
- Simulations are also blind to potentially dangerous openings that will be opened by the kibitzer. Sometimes the kibitzer assumes certain scenarios will happen frequently when in reality they will are extremely implausible.
- Simulations do not take the score or the volatility of your play into account. Computers will make the same play regardless of the score, since simulations always try to maximize equity.
- Simulations do not account for opponent tendencies.
Diagram 1:
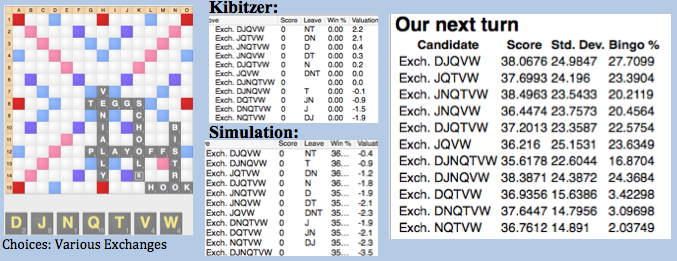
In this position, there is no way that Quackle could ever be accurate, as there are a litany of things Quackle would get wrong. First, Quackle would only fish for BENZOATE once and give up when failing to draw an E: an obviously huge mistake. Second of all, Quackle would not accurately assess how opponent would react to ALIT, TALI, or an exchange 4, assessing either how often ALIT/TALI would divert your opponent by creating a better play or how often opponent would interpret these plays as huge fishing options on column 1. Third, Quackle would do a rather poor job of assessing the need for entropy in this position, both from your point of view this play as well as your opponent’s point of view. For these reasons, a simulation would be nearly useless in determining your best option.
Quackle is unaware which words take which hooks at the end of its iterations. As a result, the simulation errantly prefers KOA because of potential plays that hook IODIZER such as RAJ/REB giving you an S hook, as well as the possibility of drawing IODIZERS yourself. Quackle overlooks the fact that this spot will often be blocked and that no human opponent will want to play IODIZER unless they need to draw the S to win.
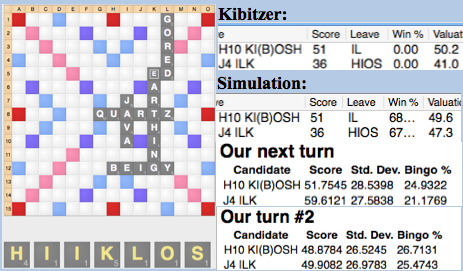
This diagram is an example of a recursion error. In this case, simulation undervalues the leave after ILK because it is much too willing to break up the OS on future turns needed for QUARTZOUS or QUARTZOSE (81 points). Even though KIBOSH wins the simulation, KIBOSH is a serious error.
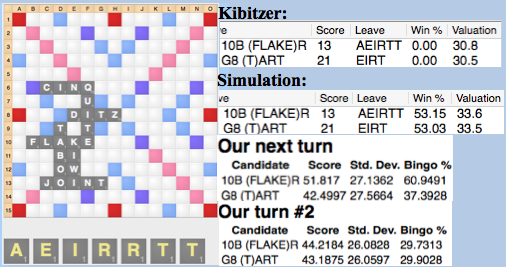
This is a similar recursion error, as the computer is unable to recognize the strength of the AEIRTT leave. On this board, there are few bingo lines available, but AEIRTT still bingos often, yet the computer will be too willing to break up this powerful leave on the next turn. Also, the computer will not infer a strong rack after either play and thus will open far too much, misestimating both plays’ bingo chances, but overvaluing TART by significantly more. Thus, fishing is a far superior play to TART, despite the simulation results.
At first, it might appear that these examples are rare. Indeed, extreme examples like the ones above are quite rare, but even for more mundane position, it quickly becomes clear that Quackle can bungle the simulation, albeit not to the same degree. This occurs especially when the simulation results are close: the simulation is not precise enough to give you a precise result.
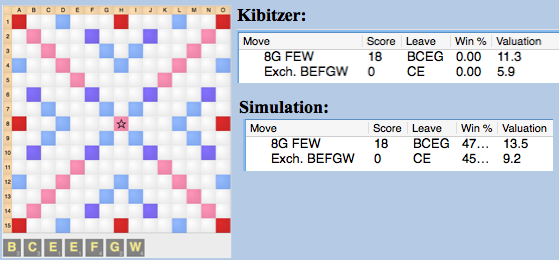
FEW wins a simulation by more than 4 points over exchanging. However, this result is contingent upon the simulation being a realistic representation of future turns of the game: the simulation must accurately project the next few turns using its kibitzer. In this position (and in many others), this does not occur: the kibitzer fails to make good plays that perform well in ensuing terms. Simulation shows that the kibitzer consistently fails to make the best play after being faced with the opening play of FEW.
In this case, Quackle does not play well because it fails to account for defense: it anticipates a much more open board than what will likely occur in a game between humans. To see how poorly Quackle plays after FEW, let’s test out a few racks that Quackle plays in response to FEW, according to the kibitzer:
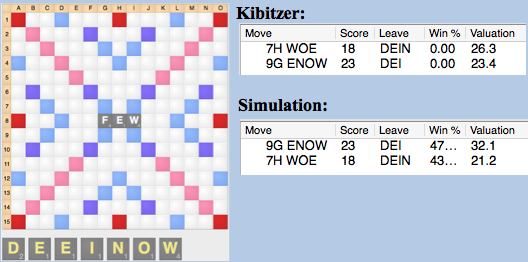
WOE 7h (18), the top play in Quackle’s kibitzer gets trounced in a sim, losing by almost 10 points in a simulation to ENOW because of its horrible defense.
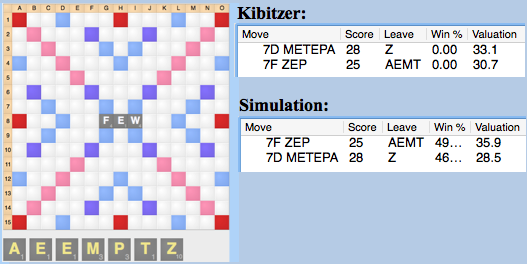METEPA 7d wins by 2.4 points in the kibitzer, but loses a simulation by 7.4
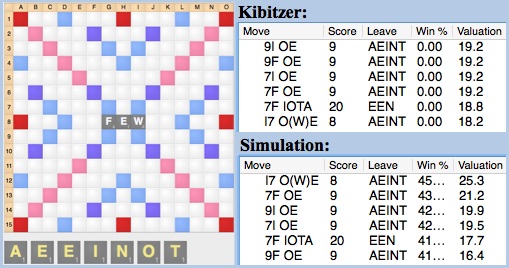
In Diagram 3, Quackle’s suggestion OE i9 gets soundly beaten in a simulation by OWE i7.
All of these racks are very different, and do not involve advanced concepts. These simulations strongly suggests that Quackle’s simulation is not accurate after FEW, and in fact will probably lead to a more beneficial situation for you since Quackle is constantly opening scoring spots that it shouldn’t. While FEW might still be the best play, there is simply too much “white noise” in the simulation to know.