(Note: This is the second installment on my series Breaking the Computer. For other articles in this series, please click here.)
Many players use computer programs for several reasons, but they don’t actually understand how these programs work, trusting those programs without understanding the inner mechanics. This is an obviously bad idea. Computer programs have limited usefulness to anyone who doesn’t understand how they actually work. Most computer programs modeling games such as poker, chess, Scrabble, and other games work in a very similar way.
Scrabble computer programs (such as Quackle) are built out of a few basic parts. The most basic unit of a computer program is called the kibitzer. The kibitzer is a module that uses a basic algorithm to quickly rank plays. In the case of Quackle, the kibitzer ranks plays according to equity (points + leave). and uses a table called Superleaves to quantify each leave. For example, with a rack like IILLPQU, the play of QUILL for 48 points retains an IP leave for a value of -2.7, for a total equity of 45.3 points.
This is all that the kibitzer does: it is a very basic calculator. It does not calculate any value for positioning whatsoever, play an endgame, or do any even remotely complicated math or evaluation. When you play beginner opponents, just the plain kibitzer is often a more basic opponent (in Quackle this is called “Speedy Player”, though speedy player also has an endgame module). And while a kibitzer might not be very complicated, it can perform these calculations extremely quickly.
A Sample Kibitzer
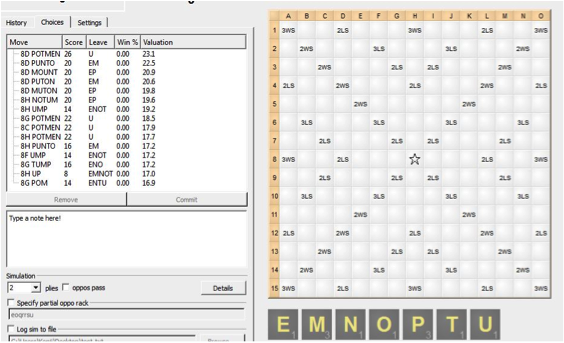
POTMEN scores 26 points – 2.9 points for the U, so the valuation is 23.1 points, while PUNTO scores 20 points + 2.5 points for the EM leave for a valuation of 22.5 points. This is how kibitzers form valuations and rank plays.
The second component is called the simulation engine. The simulation engine is also fairly simple: it randomly draws tiles for both players and runs the kibitzer multiple times, according to the user’s preferences. Simulations spit out results called valuations. Valuations are the simulation’s assessment of the worth of a play; the higher the valuation, the better the play. Simulations have two parameters: an iteration and a ply. A ply is the number of future turns you want to be considered. It is the number of “generations” that we are measuring. An iteration (or trial) is the number of times that we would like to run p plies so that we can average them.
For example, let’s say you run a two turn simulation with the same IILLPQU rack.
1. A play is made, such as QUILL for 48 points.
2. The simulation engine gives your opponent seven random tiles, for example, DDORTTY
3. The simulation engine then runs the kibitzer, specifying the best play with those tiles: in this case, ODDITY through the I in QUILL.
4. The simulation engine then draws 5 random tiles in addition to the PI leave after QUILL, for example, DENTT. It then runs the kibitzer, which specifies the best play POINTED through the O in ODDITY for 40 points.
5. Since it is now the end of this iteration, it then goes to superleaves and pulls out the value of each player’s leave, RT and T. The computer then sums up the scores and superleave values and computes a valuation [(QUILL = 48, POINTED = 40, T = ) – (ODDITY = 23, RT = )] =
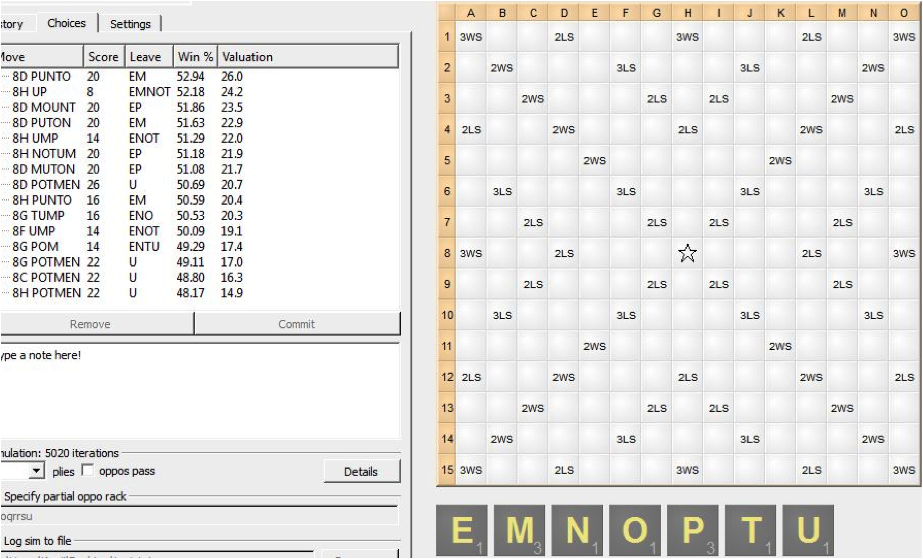
A simulation taken over 5020 iterations over 4-ply. 5000 iterations is the recommended length for simulations: it is reasonably accurate and yet does not take too long to complete. The larger the number of iterations, the more precise the simulation. In this case, PUNTO wins the simulation while POTMEN is all the way in eighth place.
Illustrations of Simulations
Example 1: Opening rack: EKNOORS (1-ply, 2 iterations)
Simulation gives your opponent two random racks and subtracts the points from your opponent’s play from the score of SNOOKER, then averages those two numbers to get a valuation.
Here we will consider playing SNOOKER at either 8c (E on star) or 8h (S on star)
Opponent Rack 1: FIILLOS
Opponent Rack 2: AADIIOU
Ply 0: SNOOKER 8h (82) Ply 0: SNOOKER 8h (82)
Ply 1: FOILS 15d (72) (LI) Ply 1: AUDIO 9e (14) (AI)
Ply 0: SNOOKER 8c (74) Ply 0: SNOOKER 8c (74)
Ply 1: FIL 9f (21) (ILOS) Ply 1: AUDIOS 3c (16) (AI)
Valuations:
SNOOKER 8h (82): (82 – 72 – {value of LI leave} + 82 – 14 – {value of AI leave})/2 = 42.85
SNOOKER 8c (74): (74 – 21 – { ILOS leave} + 74 – 16 – {value of AI leave})/2 = 55.05
(Note: the /2 term comes from the number of iterations. With 80 iterations, we would instead use /80 and use 80 racks. We want to find the average value of each iteration.)
Example 2: Opening rack AILQRUZ
Choices: QUAIL 8d (48), QUIZ 8f (44) (1-ply, 2 iterations)
(1 iteration of a 2-ply simulation with opening rack AILQRUZ)
1. Computer draws your opponent 7 random tiles
2. Computer inputs choice #1 which is QUAIL, and records it as 48 points.
3. Computer draws 5 tiles out of the bag and gives them to you, e.g. AEMOO.
4. Computer uses its kibitzer to make the top ranked play of the kibitzer using your opponent’s random rack. In this case, the random tiles were EGORSVW. The kibitzer plays, VOGUERS, and mark down 44 points.
5. Computer assessed the W leave, and creates a value for it, -3.8.
6. Computer uses your new rack to play the highest ranked play using its kibitzer. In this case, it uses your rack AELMOOZ, to make the play ORZO 10d (33). Note that this isn’t the highest scoring play.
7. Computer assesses a value for your AELM leave, +5.7.
8. Computer does math to find your valuation. In this iteration of a 2-ply sim, we get a sum of 48 – 44 – (-3.8) + 33 + 5.7 = 46.5
9. The computer starts the whole process over again with the word QUIZ, giving your opponent the rack EGORSVW to start. If there is more than one iteration, your opponent gets a new random rack and the next iteration begins. The valuations are then averaged.
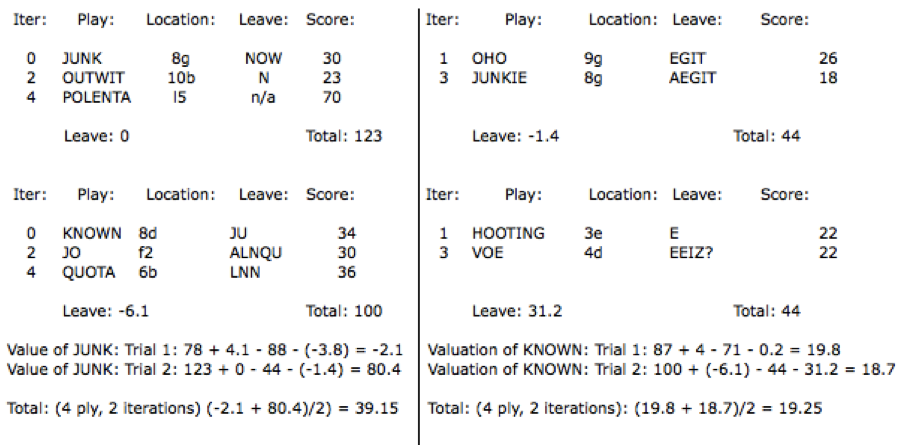
Here is a simulation in chart form:
Opening rack: JKNNOUW